
The population fluctuates around a mean of 50, but values more extreme than the range 40 to 60 are common. 5.3, where the true population size (no sampling variation) is plotted.
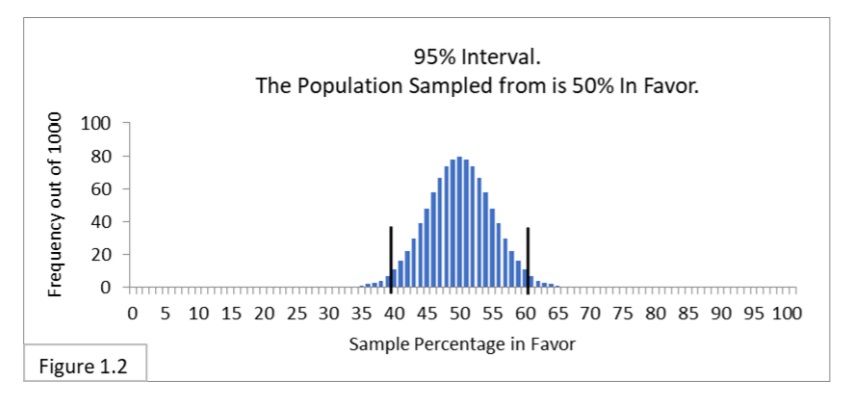
How can we determine if this reduction is important? The answer lies in determining what the variation in the owl population has been for some period of time in the past, and then if the observed reduction is outside the range expected from this past fluctuation. We would expect the size of the owl population (and any other population, for that matter) to fluctuate through time. This leads us to the second variance component associated with determining whether a trend in the population is important. 5.2), we would conclude that by chance alone, these two estimates are probably not different. Based on the overlap of the two confidence intervals ( Fig. If the 1995 estimate was N ˆ 95 = 40 with a sampling variance of Vâr( N ˆ 95) = 20, then the 95% confidence interval for this estimate is 40 ± 1.96 20, or 31.2–48.8. Then, under the assumption of the estimate being normally distributed with a large sample size (i.e., large degrees of freedom), we would compute a 95% confidence interval as 50 ± 1.96 25, or 40.2–59.8. Suppose that the 1990 estimate of N ˆ 90 = 50 pairs has a sampling variance of V a ˆ r ( N ˆ 90 ) = 25. Typically, we present our uncertainty in our estimate as its variance, and use this variance to generate a confidence interval for our estimate. We want to be sure that the two estimates are different, i.e., the difference between the two estimates is greater than would be expected from chance alone because of the sampling errors associated with each estimate. The first source of variation is the uncertainty we have in our population estimates. Two sources of variation must be assessed before we are confident of our inference from these estimates. However, if the 1995 estimate was 40 pairs, we might still be concerned, but would be less confident that immediate action is required. For example, if the population size of Mexican spotted owls in Mesa Verde National Park is determined as 50 pairs in 1990, and as only 10 pairs in 1995, we would be concerned that a significant negative trend in the population exists during this time period, and that action must be taken to alleviate the trend. Methods to separate process variation from sampling variation will be presented.ĭetection of a trend in a population's size requires at least two abundance estimates. The latter two sources often are referred to as process variation, i.e., variation in the population dynamics process associated with environmental variation (such as rainfall, temperature, community succession, fires, or elevation). Three sources of variation must be considered: sampling variation, temporal variation in the population dynamics process, and spatial variation in the dynamics of the population across space. In this section, we discuss sources of variation that must be considered to make inferences from data when trying to detect trends.
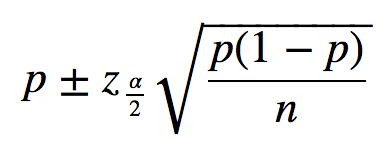
Charles Gowan, in Monitoring Vertebrate Populations, 1998 5.2 VARIANCE COMPONENTS


 0 kommentar(er)
0 kommentar(er)
